As we wrote here before (and you are already probably well aware of) – Lasers can be dangerous.
For you, for your workspace, and for your measurement equipment. Some people assume high power is the problem and low power is safe. This isn’t necessarily the case, though. What you really want to look at is the power (or energy) density of the laser. If you want to know what is power density and why it matters see our blog: Do You Know the Power Density of Your Laser?
In this Blog we’ll explain the details of how power density depends on the beam profile of your laser and how to calculate it using our power density calculator.
Beam profiles and Power Density
There are two basic laser beam profiles, Gaussian and Flat top. As the names imply, a Gaussian beam has a profile with a power distribution that follows a gaussian function. The Gaussian profile is important since it defines the basic profile of a single mode laser, other profiles are, in fact, characterized by their ‘closeness’ to an ideal gaussian using the M^2 figure of merit. An ideal Flat Top function has a profile with uniform power distribution across the entire beam, this is usually achieved with additional optics that modify a gaussian distribution.
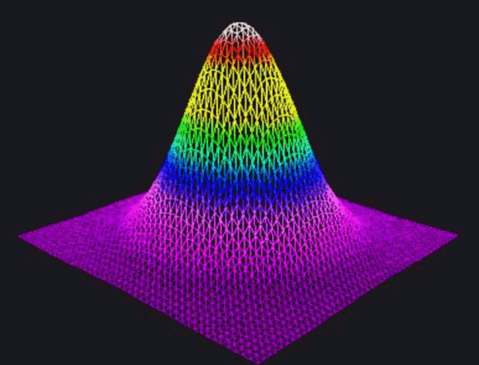
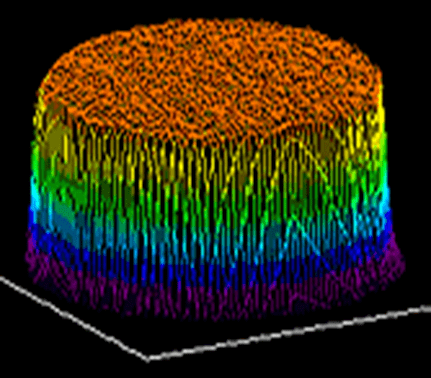
Between these two profiles there are an endless number of other profiles with unique power distributions. Here we relate only to Gaussian and Flat top profiles.
The calculation of the power density of a Flat Top profile is straight forward. You only need to take the total power, P0, of the laser and divide it by the total area of the beam, A, at the plane of interest (after taking into account the divergence of the beam), typically a Flat top beam will have either a circular or rectangular shape.
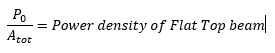
Calculating a Guassian beam power density is less straight forward since the power density changes at every point in the beam. We define a peak power density, the power density at the point in the beam with the highest power, which is usually what interests us.
As a rule, the diameter of a Gaussian beam is given in terms of the 1/e^2 of the peak power. This means that the diameter of the beam is defined by the distance between the point in the profile where the power drops to ~13.5% of the peak power at the center of the beam 86.5% of the total power is confined within the diameter defined by this point.
In order to work out the peak power density the rule of thumb is to take the total power of the beam P0 and divide it by the area defined by the 1/e^2 diameter, A1/e^2 and then multiply that by two.
![]()
This is the equivalent of calculating the power density of a Flat Top beam with the same diameter as the 1/e^2 diameter of the Gaussian and multiplying by two.
The Ophir power density calculator returns the power density of a laser beam based on the above explanations. You can define either a simple Gaussian beam or a Flat Top beam with a circular or rectangular profile. In addition, for pulsed lasers it calculates energy density based on the repetition rate of the laser and average power or the pulse energy.








Leave a Reply
Your email address will not be published. Required fields are marked *