Can a Laser Wavelength Be Converted and Why Do We Even Want to Do It?

The wavelength of a laser is a fundamental characteristic, determined by the gain medium and its internal structure.
Nowadays, one of the most common laser sources are laser diodes, whose wavelengths are determined by their design and by the materials used for their composition.

Laser diodes are driven by electrical current and directly convert electrical energy into light. Not all wavelengths can be generated from lasers with the required parameters needed for a given application, such as power or energy. When other laser wavelengths are needed, some type of wavelength conversion is typically used.  In this article we will present situations in which converting the wavelength of laser light is advantageous for specific applications, and outline processes that enable such wavelength conversion.

Tunable Lasers

We’ll start by looking at tunable lasers. The tuning range is first and foremost limited by the gain medium bandwidth. Tuning is achieved by controlling the loss in the laser cavity so that it is minimized for a certain wavelength at which lasing occurs.
The tuning mechanism can be as simple as controlling the laser’s temperature or more elaborate such as using microelectromechanical actuators to change the cavity’s length. Tunable laser diodes can be tuned to as much as 40 nm.

Solid State Lasers

Many solid state lasers, on the other hand, have a narrow gain spectrum and thus are not tunable, with the notable exception of the Ti: Sapphire laser, which thanks to its wide gain bandwidth can be tuned in the range of 650-1100 nm.

Linear wavelength

Linear wavelength conversion occurs when the laser is used to pump a gain medium, usually a crystal, to a higher energy state. The excited electrons decay to a lower energy state by emitting radiation at a longer wavelength. By placing the gain medium inside a cavity a laser is formed. A well-known example is the Nd:YAG laser, usually pumped using a laser diode at 808 nm and emitting radiation at 1064 nm. 

Nonlinear wavelength

Next we consider nonlinear wavelength conversion. In the photonics field, a system is said to be nonlinear when physical quantities, such as the polarization density P, respond nonlinearly to the electric field of the laser E. When a dielectric material is subjected to an electric field E, its molecules gain electric dipole moments and the medium is said to be polarized. The polarization density P expresses the density of these electric dipole moments, and it can be described using the following equation:

•  P = e₀(c⁽¹⁾E + c⁽²⁾E² + c⁽³⁾E³ + …),

where e₀ is a constant and c⁽ⁿ⁾ are called the n^th-order susceptibilities of the medium, indicating the degree of polarization of a dielectric material in response to an applied electric field E.  This equation suggests that if an electrical field E excites the medium, a polarization proportional to E² is created, and its magnitude is related to the term c⁽²⁾. If E oscillates with frequency ω, then P has a component that oscillates at 2ω. In simple terms, in response to excitation at frequency ω, we get electric dipoles oscillating and radiating at frequency 2ω. So in fact, the medium converts radiation at ω to radiation at 2ω.
This is called second-harmonic generation (SHG). A well-known example of second-harmonic generation is the 532 nm green laser that uses a nonlinear crystal to convert 1064 nm to 532 nm via SHG. A commercial laser source which relies on this process is Spectra Physics VGEN-G fiber laser, presented in Fig. 1, which includes a SHG module to generate a pulsed green laser beam.

A typical nonlinear optical process relies on an intense and well-polarized laser beam and a nonlinear medium that is capable of supporting it. Nonlinear optical processes differ in the operating laser conditions they require, the nonlinear media, and the degree of the susceptibility c⁽ⁿ⁾ used in the process.
Many nonlinear processes result in radiation with a narrow wavelength range, but that is not without exception; a supercontinuum light source, for example, typically uses a sophisticated optical fiber structure to convert an optical pulse into ultra-broadband radiation, which contains an extremely wide wavelength range. More details on this subject can be found in the MKS website.

In order for the nonlinear medium to efficiently generate coherent radiation, certain conditions need to be met, known as phase-matching conditions. Phase matching implies that proper phase relations between the interacting waves at different frequencies will be maintained inside the nonlinear medium. Only if these conditions are fulfilled do we obtain coherent radiation, resulting from the sum of nonlinear processes that occur during the light’s propagation inside the medium. The basic phase-matching equation is:

• k₃ = k₁ + k₂,

where k are the wave vectors of the light, and the subscripts represent the interacting beams. For SHG the subscripts 1 and 2 are of the original laser light, and the subscript 3 is of the newly-generated wave with twice the frequency. Figure 2 shows an illustration of an SHG process, in which infrared light is converted into green. Note that the conversion efficiency of nonlinear processes is limited so part of the incoming light passes through the nonlinear medium without changing. In this context it is worth focusing on pulsed lasers: when working at short pulses, the instantaneous power can be extremely high compared to a continuous wave (CW) laser with a constant average power. The high instantaneous power increases the efficiency of the nonlinear process.

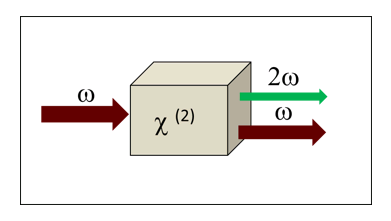
Though fulfilling the phase-matching conditions basically means conserving energy and momentum, it turns out that converting the light’s wavelength efficiently using SHG requires careful design of the nonlinear medium. Why is that? If we assume collinear propagation (so that Eq. 2 becomes scalar) and set k₁=k₂ (since these wave vectors originate from the same laser beam), we get the equality k₃ = 2k₁. Substituting the definition of k = 2pn/l, where n is the refractive index and l the wavelength of light, results in the condition n₃ =n₁, since l₃ = l₁/2. This means that the original and newly-generated waves should have the same refractive index inside the nonlinear crystal. However, it is rarely the case that a material has a fixed index of refraction over such a wide spectral range.
Therefore, in order to achieve phase matching, the nonlinear medium has to also be birefringent, i.e., with refractive indices that depend also on the polarization and the propagation direction of the beams inside the crystal. 

Thus, by carefully cutting the nonlinear crystal at specific angles and sometimes by controlling its temperature (since the refractive index is temperature-dependent as well), it is possible to fulfil Eq. 2, because the k vectors originate from different dispersion curves.

Examining again Eq. 1, we realize that other nonlinear processes are possible: sum- and difference-frequency generation, third-harmonic generation, and others. Sum- and difference-frequency generation are processes in which the sum and difference of two input frequencies are generated. They rely also on c⁽²⁾ nonlinearity, and in fact SHG is a special case of sum-frequency generation, for which the two input waves share the same frequency. Third-harmonic generation, in contrast, relies on c⁽³⁾ nonlinearity, and allows generation of light with triple the frequency of the original beam.
To obtain a laser at a wavelength of 355 nm from a 1064 nm laser it is possible to generate third-harmonic generation using a single crystal. However, it turns out that since most materials have low c⁽³⁾ nonlinearity compared to c⁽²⁾, it is more efficient to use a first crystal to generate 532 nm light via SHG and then guide the second harmonic and the residual 1064 nm beams to a second crystal to obtain 355 nm laser via sum-frequency generation.
It is important to note that the two crystals used for these processes are not identical, as each crystal mixes different wavelengths and therefore needs to be tailored specifically for the desired nonlinear process it supports.

Non-coherent laser-driven light sources

Last, we consider non-coherent laser-driven light sources. A well-known example is light-emitting plasma excited by laser radiation: a laser can excite plasma in Xenon lamps, creating a broadband source in the visible part of the spectrum. Another example of a non-coherent light source is the generation of plasma that emits Extreme Ultra Violet (EUV) radiation at a wavelength of 13 nm. The plasma is generated by focusing a high-power CO₂ laser, at a wavelength around 10 µm, on tin droplets in vacuum. Here only a small fraction of a multi-Kilowatt laser is converted into 800-times shorter wavelength radiation. The resulting EUV light enables the most advanced photolithography processes used in the microelectronics industry.

When faced with an application that requires incorporating a laser, both the wavelength and the laser’s operation mode are considered. For metal welding, for instance, high-power CW laser is required, in order to heat the metal to its melting point and join metal parts together. Short wavelengths, such as 355 nm or 266 nm, are preferable for this application, since the light absorption in metals increases significantly as the wavelength decreases. Laser engraving, in contrast, requires the use of pulsed lasers, since it relies on high instantaneous power to mark the object’s surface, and does not require the generated heat to penetrate deep into the material. Similarly to the previous example, the laser wavelength should be chosen according to the material of the sample for optimal performance.

In conclusion

It is not always possible to get the optimal wavelength we desire for a specific application – the limitations arise both from the lasing mechanism itself, and from the availability of nonlinear materials and processes which are able to convert the laser’s wavelength.
Nevertheless, the incorporation of nonlinear optical elements enables the laser industry to reach far into more wavelength regions with constantly improving capabilities. In some cases, it allows industrial or scientific processes that are otherwise impossible to attain. In other cases it can improve manufacturing yield and performance of various laser-based systems.