If you always wanted to learn an easy way to calculate power density –without even using our calculator, even in your head, this is the perfect blog post for you.
In this Blog we’ll explain the details of how to calculate it using our power density calculator.
If you don’t want to damage any of your instruments, make sure you know your laser’s power density. If you aren’t sure what it is, you can use this power density calculator.
Let’s start with a definition: power density is power per unit area which is usually expressed in terms of W/cm^2.
The Calculation of power density is pretty simple – composed of 2 steps:
- Calculate the area of a beam using the radius in cm
- Divide the beam’s power by that area
And there you have it – You’ve just obtained power density in units of W/cm^2.
However…
Since beam size is usually given with the beam diameter in terms of millimeters, to calculate power density in W/cm^2 you will also have to:
- Convert the diameter to cm,
- Divide the diameter by two to find the radius,
- Use πr^2 to find the area in cm^2
- And, finally, divide the laser power by the area to obtain power density
This calculation can be a bit tedious and time consuming, especially for technicians and field engineers who want to make as quick and easy a calculation as possible.
How can I make it easier for you?
Glad you’ve asked!
Using the following formula you can directly find power density of a laser beam using the diameter of the beam in millimeters:
Here is how this equation is derived: We can write an expression for the power density of a 1 mm diameter beam, which is simply:
Dividing the expression of power density of a 1 mm beam — Power / π(0.5mm)^2 — by an expression of power density as a function of diameter — Power / π(0.5d)^2 — we find that the ratio is d^2. Thus, power density as a function of diameter can be expressed as the power density of a 1 mm beam divided by d^2:
Note: This formula assumes the beam is a flat top beam where the beam power density is uniform.
For a Gaussian beam with a given beam waist in mm, multiply this formula by two to obtain the formula given above (The multiplication factor is due to the fact that for a Gaussian beam, the peak power in the center is twice the average power density of the beam. The value is actually closer to 255, not 250, but this difference is trivial, introducing only ~2% error. We use 250 simply because it’s easier to remember and perform mental calculations than 255! )
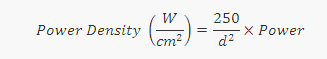
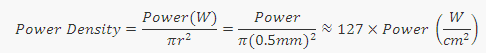
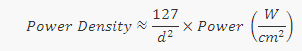












Leave a Reply
Your email address will not be published. Required fields are marked *