Meet the Optical Vortex

What would it take to fully characterize a general beam of light?

To begin we would probably specify its color or, more accurately, its spectral distribution.
We would also need to describe its spatial distribution, i.e. the intensity versus position in a cross section of the beam. But light, of course, is a vector phenomenon so our characterization would also need to include the direction of the electric and magnetic fields (polarization).

And we are not done yet.

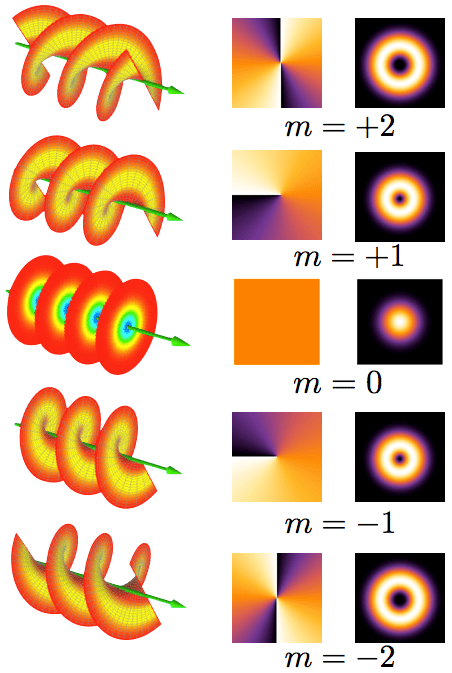
In addition to varying in intensity, different points of the cross section can vary in phase relative to each other. As we traverse a ring centered on the beam axis, the total phase change can be integer multiples of 2 (preserving continuity over the full circuit). For integers other than zero, the wavefront is said to contain an optical vortex.

There are physical quantities associated with these properties. Wavelength correlates with the quantized energy of the field as well as its momentum. Photons with circular polarization carry angular momentum as well. Beams with vorticity also carry angular momentum. For collimated beams the angular momentum from polarization and that due to the wavefront interact with matter differently. It is therefore useful to distinguish between them.

The angular momentum due to polarization is usually referred to as light spin angular momentum (SAM) while that due to the shape of the wavefront is called light orbital angular momentum (OAM).
Somewhat surprisingly, the richness afforded by OAM states only began to receive significant attention fairly recently. The beginning of serious research into OAM states is usually traced to a seminal paper by Allen, Beijersbergen, Spreeuv and Woerdman from 1992, almost 3 decades after research into non-linear optics exploded after the invention of the laser.

Perhaps the delay can be attributed to the dearth of well-defined OAM states found in nature. In fact, most research is based on several techniques developed to allow the creation of custom OAM states on demand. Starting with a beam of uniform wavefront, the desired phase variation is added using devices such as a “forked” hologram, a spiral phase plate or a Q-plate.

Applications exploiting these novel optical states are currently in the research stage. Applications being considered include use as another dimension for multiplexing in communication systems, remote physical manipulation of particles in optical tweezers, added dimensions for entanglement in quantum computing, and advanced sensing (possibly direct imaging of exoplanets using an optical vortex coronagraph).

Despite the simplicity of Maxwell’s four little equations, we are apparently still far from exhausting their subtle complexities and the complex phenomena they encompass.

For further reading (based in part on http://www.astro.lu.se/ALVA/old/photon_oam.html)

All Screwed Up, Scientific American. November 3, 2003. Link
“Optical Vortices” Might Extract Abundant Information From Matter, AIP; Physics News Update, Number 721. Link

Twisting the light away, New Scientist, Issue 2451. June 12, 2004.
Light’s Orbital Angular Momentum. Miles Padgett, Johannes Courtial & Les Allen. Physics Today, May 2004.
Orbital Angular Momentum (OAM) of light beams and photons, C. Barbieri, http://www.icranet.org/download/ESOP/Slides/barbieri2.pdf

Light in a Twist: Orbital Angular Momentum, Miles Padgett, http://www.gla.ac.uk/media/media_263851_en.pdf
https://en.wikipedia.org/wiki/Orbital_angular_momentum_of_light , https://en.wikipedia.org/wiki/Optical_vortex , https://en.wikipedia.org/wiki/Angular_momentum_of_light