The Focal Spot Size Calculator

It is not uncommon in working with lasers to need to focus the laser beam down.

When using a lens, our first impulse is to fall back on the thin lens equation we learned in geometric optics.

In fact, that equation is applicable to spherical waves in the paraxial approximation. It is not reliable for Gaussian beams, especially when working in the near field (defined as distance from the waist, z < z_R, the Rayleigh length, to be defined below). In fact, the location of the new waist will be shifted relative to that expected from using the geometrical thin lens equation.

A spherical TEM00 mode Gaussian beam is characterized by two parameters, e.g. the waist, w₀, and the divergence, q_FF. Alternately, the Rayleigh length, z_R, (AKA Rayleigh range) or the wavelength, l, can be substituted for one or both of the above. The Rayleigh length is defined as

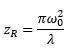
where l is the wavelength and w₀ is the beam waist.

Focal Spot Size Calculator

There are matrix methods that can be used for propagating the diameter and curvature of the beam, but if your main interest is simply the location of the new focus (i.e. beam waist) or the size of the focal spot, you can use the Focal Spot Size Calculator tool on the Ophir website.

This tool uses the equations derived by Sidney Self which take a form reminiscent of the geometric optics (Gaussian) thin lens equation. [SA Self, Applied Optics 22(5), 1983, pg 658-661] In normalized form, the thin lens Self equation is

where s is the object distance, s’ is the image distance, f is the focal length of the lens and z_R is the Rayleigh range of the laser beam. Object and image distances refer to the locations of the beam waist before and after the lens.

Several important insights can be gleaned by analyzing this equation.

The first is that it approaches the geometrical optics thin lens equation in the limit (z_R/f)à0.

On the other hand, a beam with a waist at the front focal plane of the lens will reach a new waist at the back focal plane, independent of the Rayleigh length. This is very different from the geometrical optics case in which an object at the front focal plane is imaged at infinity. Conversely, for object distances that are not exactly at the front focal plane but near it, the image distance is strongly dependent on the Rayleigh length.

In fact, there is no object distance that produces a beam waist at infinity. For a positive lens, the waist will always be imaged at a finite distance beyond the lens (except for a small range of parameters in which the image distance is negative – but still finite).

For a positive lens and real object, the maximum image distance, s’ =  f + f²/2z_R is achieved at an object distance of s = f + z_R. The minimum image distance s’ =  f – f²/2z_R occurs for s = f – z_R.

While a more detailed analysis, which can be found in Self’s beautiful 1983 article, is insightful and rewarding, practitioners needing to save time are invited to use Ophir’s Focal Spot Size Calculator.