Integrating Spheres, Pulse Stretching & Asymmetry

One of the really useful features of integrating spheres is that they can have multiple detector ports. Thus, more than one detector can be attached to make different measurements in parallel. As for all measuring devices, we need to understand the nature of the device,because it can affect the measurement results.

Stretch short pulses

One aspect of integrating spheres that should to be taken into consideration is that they stretch short pulses.  The reason for this is very straightforward. Light that enters an integrating sphere bounces around many times, overlapping on itself.
For example, with a 135 mm diameter sphere, if the light bounces around 20 times, it travels in total 2.7 meters which takes 9 ns. (Calculating the actual amount that pulses are stretched is a little more complicated than this.)

Obviously, the amount of pulse stretching will depend on the size of the sphere and how many times light bounces around inside it. The sphere time constant, t, is a function of the sphere diameter and the factors that contribute to losses (port areas and wall reflection less than 100%).

Pulse’s rise time and fall time

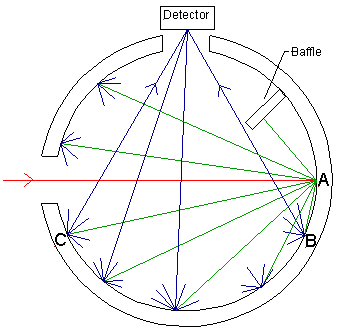
What’s less obvious is that the stretching phenomenon affects the pulse rise time and fall time differently. To understand this, let’s look at how light propagates inside the sphere.
Take for example a short light pulse that enters an integrating sphere in a collimated beam. The beam hits the sphere surface at point A and diffuses out fairly uniformly over the almost the entire sphere inner surface except where it is shadowed by the baffle. (This is the purpose of the baffle, to prevent light from the first bounce of a collimated beam from reaching the detector directly).

The light continues to bounce around in the sphere many times as it is slowly attenuated by escaping from one of the ports or being absorbed by the sphere walls.  Light from the second bounce and onward reaches the detector.
Since the surface area of the sphere within the detector’s field of view (from point B to point C) is already fully illuminated by the second bounce, the detector signal will reach its peak level relatively quickly.
The rise time will only be stretched because light traveling from point A to the detector will arrive longer if it travels via point C than if it travels via point B. The fall time on the other hand will be determined by the rate of attenuation of the pulse as it bounces around in the sphere.

To conclude…

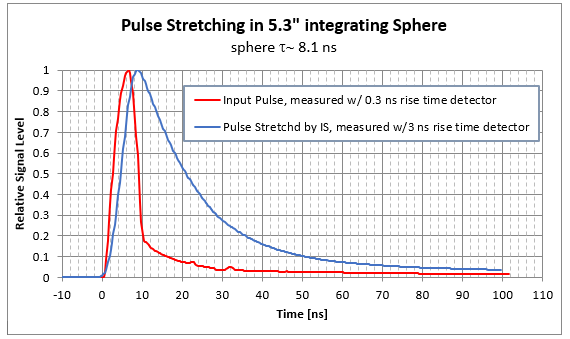
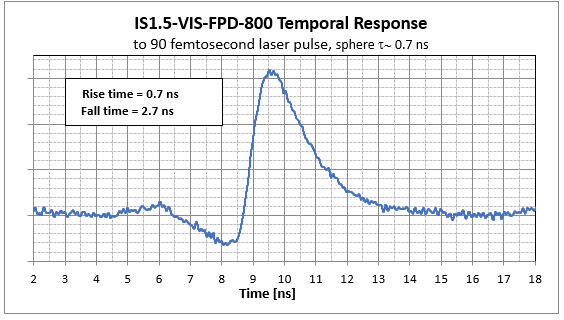
As we can see in the graphs below, the integrating sphere will have a smaller effect on the pulse’s rising edge and a much larger effect on its falling edge.
Any time we need to measure the pulse characteristics of pulses with widths less than 100 ns, we need to consider the pulse stretching effect of the integrating sphere. For very short pulses, small diameter integrating spheres like the IS1.5-VIS-FPD-800 should be used.