“She’s as focused as a laser.”
We’ve all heard similes like this one, but we also know that as straight as a laser beam seems, it’s not 100% focused. Every real laser has some divergence, as small as it may be, and keeping this divergence under control might determine whether a part is passed or failed or even the success of medical procedure, depending of course on your particular laser application.
BeamGage, with the use of any of Spiricon’s Beam Profilers, has three options for measuring divergence:
- Focal Length Method
- Far-Field Wide Angle Method
- Far-Field Two Point Method
Only the focal length method is ISO compliant, but you should be able to achieve a similar level of accuracy with any of the above measurement methods. Another consideration is that you’ll need a focusing lens for the first method, while the other two methods need no lens – however, you’ll be measuring them in the far-field, so be sure you have enough space.
Now that you have decided which method is right for you, let’s see how the actual measurement is performed:
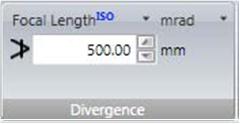
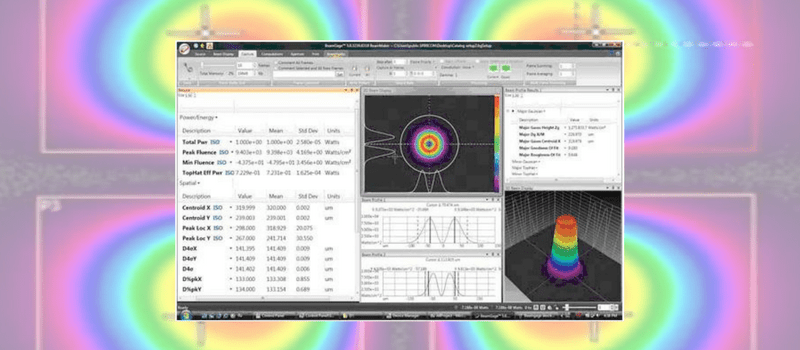
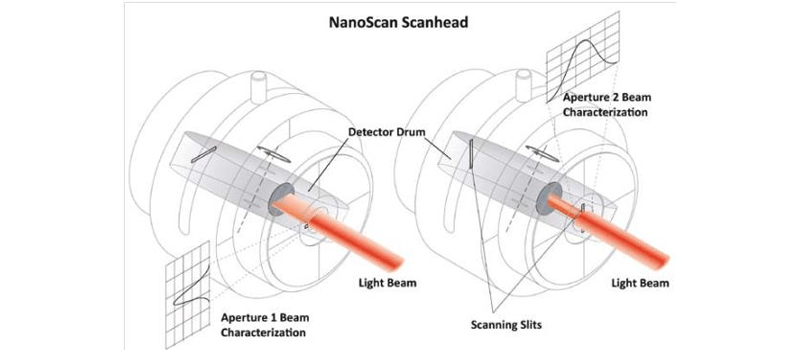
1. Focal Length: You will need: your laser (duh), a focusing optic, and your beam profiler. The optic can be refracting or reflecting, but take care that its diameter is much larger than the beam to prevent any diffraction effects from occurring. You will need to enter the focal length of this optic in the divergence panel as shown:
Now, place your beam profiler at the focal point of the lens and BeamGage will calculate your laser’s divergence, using the following formula:
divergence = tan-1 ( beam width / focal length )
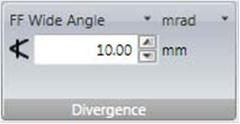
2. Far-Field Wide Angle: This method is well suited to rapidly-diverging laser beams. If your beam diverges more in one direction than another, we recommend rotating the detector so its wider side lines up with the rapidly diverging axis of the beam. In any case, place the beam profiler close enough to the laser that the beam doesn’t overfill the detector. The rest of the measurement is just like using the focal length method, but here fill in the distance from the laser to the camera instead of the focal length:
The formula used here is also slightly different:
divergence = 2 ∙ tan-1 [ beam width / (2 ∙ distance) ]
3. Far-Field Two Point: This last method actually compares the beam width at two points to find the divergence. As such, the camera will need to be placed at two spots, giving BeamGage a chance to take beam width measurements at both points. The only distance that needs to be entered is the distance between the two measurement points. Once you’ve got that, BeamGage will use this formula to calculate divergence:
divergence = 2 ∙ tan-1 [ ( second beam width – first beam width ) / (2 ∙ distance) ]
Note that “distance” here refers to the difference between the two points as opposed to the distance to the source, as in the previous two examples.
I hope that now that you’ve spent the few minutes necessary to keep track of your laser beam divergence, you’ll be able to spend more time using your laser and less time worrying about it.
You might also like to read: BeamGage user guide for more information on measuring divergence.
And measuring widely diverging beams






Now, place your beam profiler at the focal point of the lens and BeamGage will calculate your laser’s divergence
Please ignore previous post, it was sent prematurely.
In the focal length method above, it is stated that this method will calculate “your laser’s divergence”. This means that the larger the beam size, the larger the divergence?
This doesn’t make sense, because a smaller laser beam will always diverge faster than a larger beam.
So where is the anomaly?
Thanks,
Christo Liebenberg
Hi Christo, thanks for your question.
If the laser beam were totally parallel, the beam would focus at f, so divergence = tan^-1 (0/f) = 0.
If the laser is diverging, the beam will focus after f, since the lens needs to do extra “work,” to collimate the laser and then further to focus it. When we measure beam width at f, the laser isn’t yet focused, so we get a positive divergence from the equation, depending on the size of the laser at f.
The higher the divergence, the farther the focal point gets past f, which means the beam size measured at f will be larger, giving us a higher value.
Dr. Paschotta has a short, clear explanation here:
http://www.rp-photonics.com/focal_length.html
In the section titled: “Focusing of Divergent Beams”
Hope that helps clear some things up and apologies for the delayed response – it was a tough question!
i want to buy a lens or a system to collimate and rotate the elliptical laser diode beam of divergence angle in the vertical axis is 25 degrees and horizontal is 10 degrees to be 1.8 to 2.2 mrads in horizontal and 0.67 to 0.83 mrads in vertical
thanks